Our Very Own Graph Theory Book: MATH 795, Fall 2020

Let \(G=(V,E)\) be a bipartite graph. Let \(M\text{,}\) a subset of \(E\text{,}\) be a matching of \(G\text{,}\) meaning every vertex of \(G\) is incident with at most one edge in \(M\text{.}\) Let \(U\text{,}\) a subset of \(V\text{,}\) be a vertex cover, meaning every edge of \(G\) is incident to a vertex of \(U\text{,}\) alternatively, the subgraph \(G\setminus U\) will have no edges. To make this proof easier to follow let \(m(G)\) be the number of edges in the maximum matching of \(G\) and \(c(G)\) be the number of vertices in the minimum vertex cover of \(G\text{.}\) We will show that \(m(G)=c(G)\text{.}\)

Let \(G\) be a minimal counterexample,

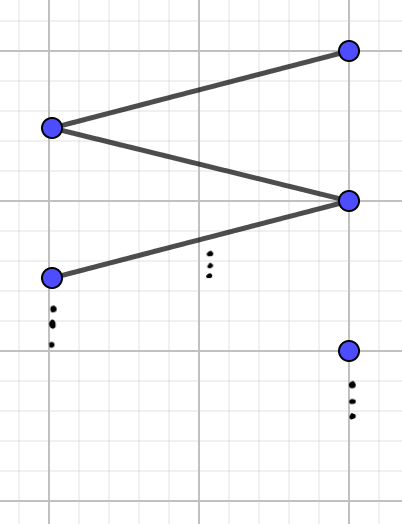
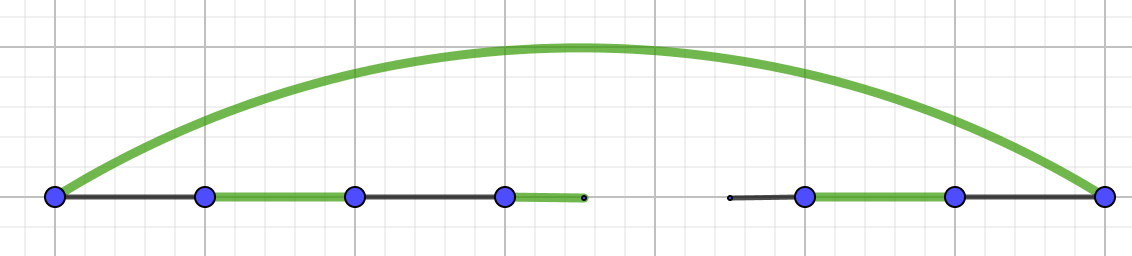
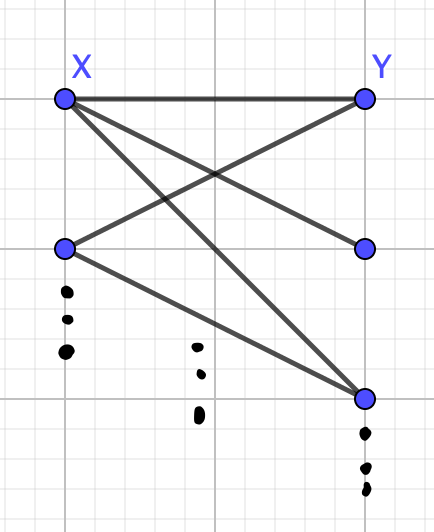
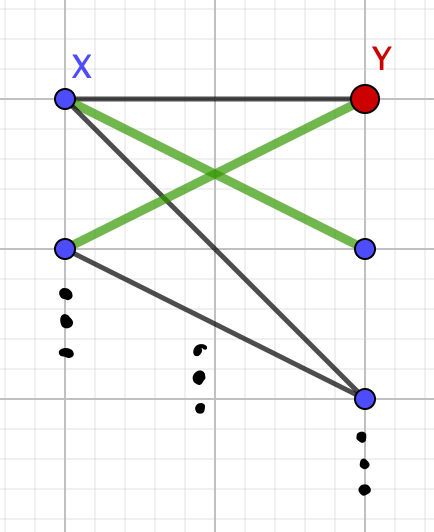
In both cases we reach contradictions, hence \(m(G)\) cannot be strictly less than \(c(G)\text{.}\) So, we can conclude \(m(G)=c(G)\) when \(G\) is bipartite.

First, consider the forward direction of Hall's Theorem and let \(G\) be a bipartite graph with \(|A| = |B|\) have a perfect matching. We will show that \(|N(S)| \ge |S|\) for all \(S \subseteq A\text{.}\) This is true somewhat trivially. If \(G\) has a perfect matching then each \(s \in S\) is matched with some vertex in \(B\) such that \(|N(S)| = |S|\text{,}\) so the condition is satisfied.

Second, consider the backwards direction of Hall's Theorem and let \(G\text{,}\) a bipartite graph with \(|A| = |B|\text{,}\) satisfy \(|N(S)| \ge |S|\text{.}\) We will show that \(G\) has a perfect matching. Suppose not, such that \(G\) satisfies \(|N(S)| \ge |S|\text{,}\) but a perfect matching does not exist. By considering the maximum matching, we know \(\exists a \in A\) such that \(a\) is unmatched. Now consider all alternating paths in \(G\) that start at \(a\text{.}\) Let \(X=N(a)\subseteq B\) and \(S=N(N(a))\subseteq A\text{.}\) There then cannot exist a maximal alternating path that ends at a vertex in \(B\text{,}\) otherewise that would be an augmenting path that would increase our matching. Thus every vertex in \(X\) is matched to a vertex in \(S-\{a\}\text{.}\) Similarly, every vertex in \(S-\{a\}\) is matched to a vertex in \(X\text{.}\) So, we then have a bijection between of \(S-\{a\}\) and \(X\text{,}\) and so \(|S| = |X+1|\text{.}\) But \(N(S)\subseteq X\text{,}\) so let \(b\in B\) be connected to a vertex \(s \in S\text{.}\) The edge \((s,a)\) must be in our matching or else \(s\) is adjacent to \(b\) by an alternating path that doesn't contain \(a\text{.}\) We can take that alternating path ending in \(B\) and extend it with \(b\text{,}\) yielding an augmenting path and therefore a contradiction. Hence \(b\) must be in \(X\text{,}\) and so \(|N(S)| \le |X| = |S| − 1\text{.}\) Therefore \(|N(S)| ≤ |S|\text{,}\) and \(G\) must have a perfect matching.

For \(|A|=1\) the theorem holds. Assume that for \(|A| \ge 2\) there is a perfect matching if \(|N(S)| \ge |S|\) for all \(S \subseteq A\text{.}\)

If \(|N(S)| \ge |S| +1\) for all non-empty set \(S \subset A\) then pick an edge \(ab \in G\) and consider the graph \(G' = G - \{a,b\}\text{.}\) Then for every non-empty set \(S \subseteq A \setminus \{a\}\) we have that \(|N_{G'}(S)| \ge |N_G(S)|-1 \ge |S|\text{.}\) So by assumption \(G'\) contains a matching of \(A \setminus \{a\}\text{.}\) Adding in the edge \(ab\) produces a matching of \(A\) in \(G\text{.}\)

Now suppose there is some non-empty proper subset, \(A'\) where \(|N(A)| \not\ge |A| +1\text{.}\) By assumption \(|N(A)| \ge |A|\) so it must be that \(|N(A)| = |A|\text{.}\) Let \(B' = N(A')\text{.}\) By assumption \(G' = G[A' \cup B']\) contains a matching of \(A'\text{.}\) If we consider \(G - G'\) there cannot be any set \(S \subseteq A \setminus A'\) with \(|N_{G-G'}(S)| \lt |S|\) because that would mean \(|N_G(S \cup A')| \lt |S\cup A'|\text{.}\) So then by assumption \(G-G'\) contains a matching of \(A \setminus A'\text{.}\) Putting the two matching togethers produces a matching for \(A\) in \(G\text{.}\)

Let \(G=(A,B,E)\) be a bipartite graph such that \(|N_{G} (S)|\geq |S|\) for all \(S\subseteq A\text{,}\) and assume for the sake of contradiction that the size of a minimum vertex cover is not \(|A|\text{.}\)

By Theorem 6.0.4, the size of such a minimum vertex cover is equal to the size of a maximum matching. But a maximum matching has size at most \(|A|\text{,}\) so we have that the size of a minimum vertex covering of \(G\text{,}\) call it \(U\text{,}\) is strictly less than the size of \(A\text{;}\) i.e., \(|U|\lt |A|\text{.}\)

Then for \(A'\subseteq A\text{,}\) \(B'\subseteq B\text{,}\) let \(U=A'+B'\text{.}\) Then we have that \(|A'|+|B'|=|U|\lt |A|\text{.}\)

Thus \(|B'|\lt |A|-|A'|=|A\backslash A'|\text{.}\) Let \(S=A\backslash A'\text{.}\)

Now \(U\) is a covering of the edges of \(G\text{,}\) so for any vertex \(v\in A\backslash A'\) there must be no an adjacent vertex \(b\in B\backslash B'\text{.}\) This implies that \(N_{G} (S)\leq |B'|\lt |S|\text{.}\)

But this violates the assumption that \(|N_{G} (S)|\geq |S|\) for all \(S\subseteq A\text{,}\) and we have a contradiction. Thus the size of a minimum vertex cover must be \(|A|\text{.}\)