Computable Graphs

Section 7.2 Computable Graphs

Definition 7.2.1.

A graph is computable if there is some algorithm wich determines if vertices are adjacent.

Definition 7.2.2.

A graph is highly-computable if is computable and there is an algorithm to determine the dgree of a vertex.

There are a number of ways to make the idea of computability more formal. For our purposes these are not necessary and we will work with an infromal notion of computability.

Note that the two theoroms we proved about infinite graphs certainly apply to computable graphs. A natural question to ask is if the proporties are also computable. I.e., We know that if all of the finite subgraphs of a computable graph are $k$-colorable then the graph is $k$-colorable; is the $k$-coloring computable? Similarly, we know that a bipartite graph $G$ has an $A$-perfect matching if it satisfies Hall's condition; is the $A$-perfect matching computable?

Unfortunately, there are computable graphs with $k$-colorings where the coloring is not computable. In fact we will construct a computable graph that is 3-colorable but does not have a computable coloring. The construction we will use can be thought of a game where one player is constructing the graph and the other player is coloring the graph. Here is how the game is played: The players will alternate turns. Player 2 is attempting to use the fewest number of colors possible. Player 1 will construct the graph in such a way that player 2 is forced to use a new color on every turn.

Player 1 presents a chain of four vertices, $v_1,v_2,v_3,v_4\text{,}$ with edges $v_1v_2,v_2v_3,v_3v_4\text{.}$ Player 2 must color $v_1$ and $v_2$ with two alternate colors, say color 1 and color 2. These vertices will be called the first and second witnesses.
Player two may choose to use a third color for $v_3$ in which case $v_3$ would be the third witness. If player 2 instead uses colors 1 and 2 on vertices player 1 then adds a new vertex, $v_*\text{,}$ along with edges $v_*v_3\text{.}$ Clearly player 2 must now use a third color. In this case $v_*$ is the third witness.
Suppose that for a chain of $i \ge 4$ vertices, $v_1, v2, ..., v_{2^{i-2}}$ player 1 can add vertices to force $i-1$ witnesses. Player 1 can force another witness by duplicating this strategy above another chain of vertices (creating a new set of $i-1$ witnesses). Player 2 may choose to use a new color on one of the vertices. If not player 1 can add an additional vertiex connected to all of the new witnesses creating an $i$th witness. Repeating this strategy playwer 1 can force $k$ witnesses on a chain of $2^{k-1}$ vertices.

In the following activity you will familarize yourself with the game by playing a few rounds. You will take the role of player 1. You will be presented with a move made by player two and respond according to the rules above.

Activity 21.

(a)

Suppose that you have presented four vertices and player 2 has colored them using two colors. What do you do?

Solution

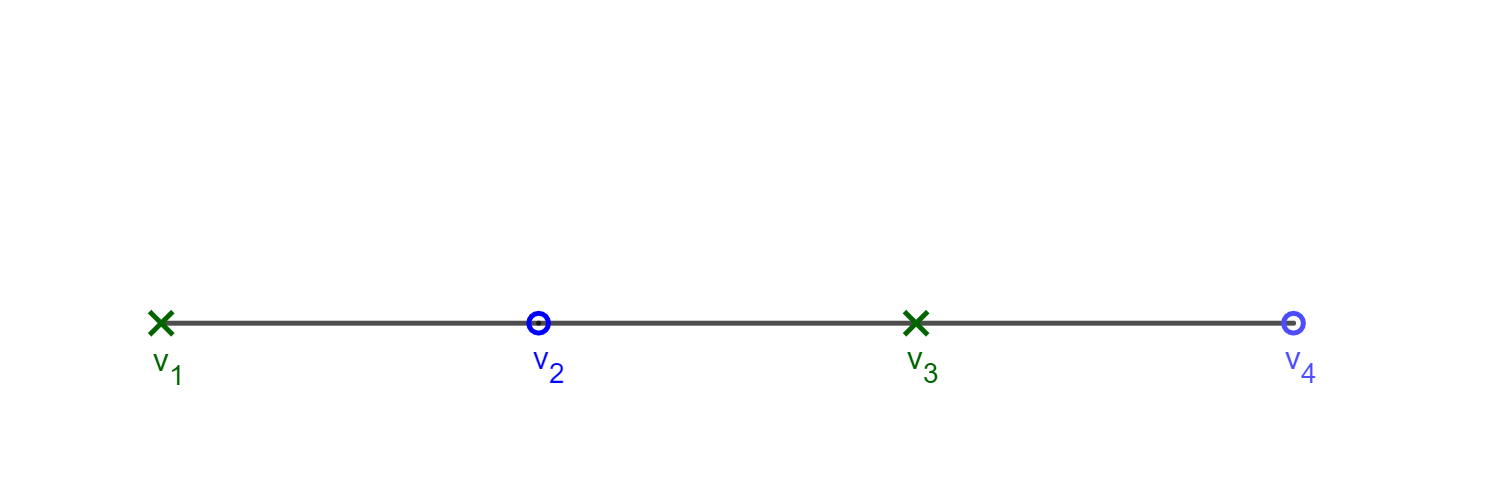
You would label the first two vertices as the first two witnesses. Then you would add a vertex above and connected to the last two vertices. On their next turn player two will be forced to use a third color on this vertex.

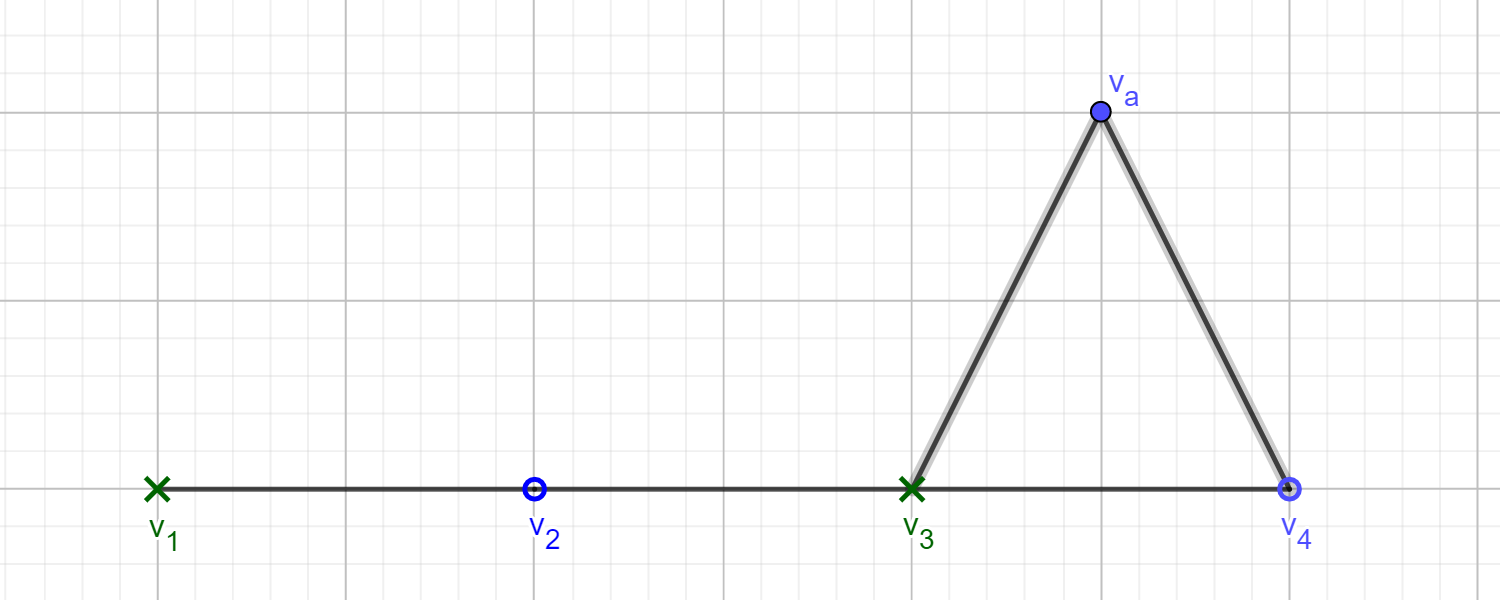
(b)

Suppose that you have presented four vertices and player 2 has colored them using three colors. What do you do?

Solution

You label the three vertices with unique colors as the first three witnesses. You will then present player two with a chain of four new vertices.

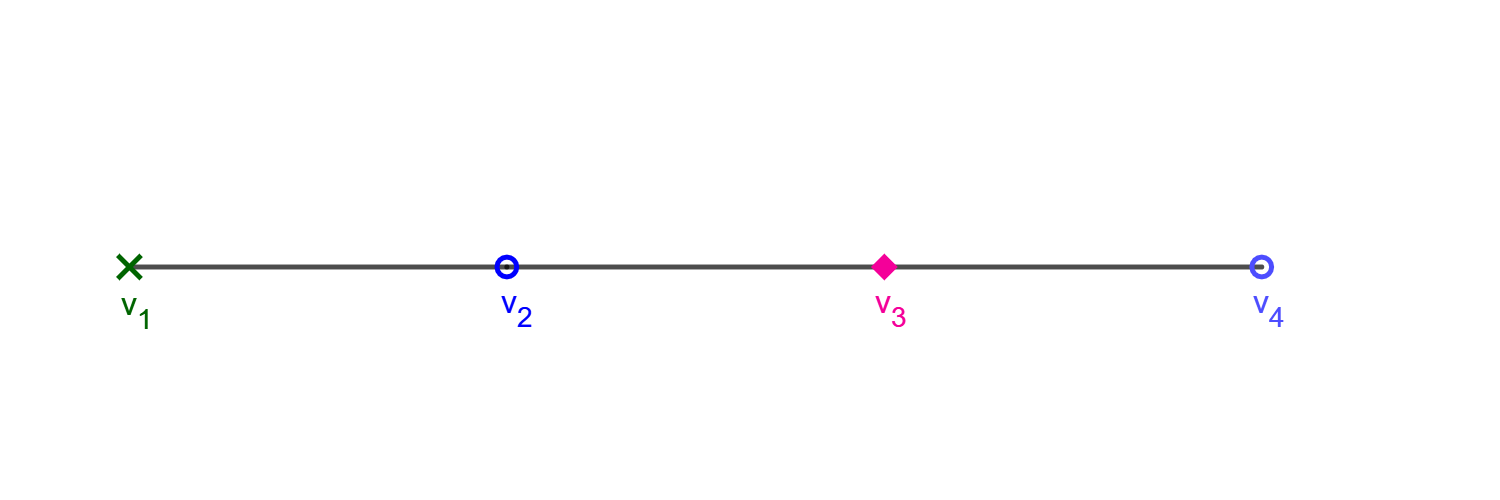
(c)

Suppose that after the move above player 2 uses two existing colors on the new chain of vertices.

Solution

Since player 2 has not used a new color you do not yet have a new witness vertex. You will continue with your strategy and add another vertex above the last two. If player 2 uses a new color on this vertex you lable it as the third witness. If player two does not use a new color then you add an additional vertex and connect it to the existing witness vertices.

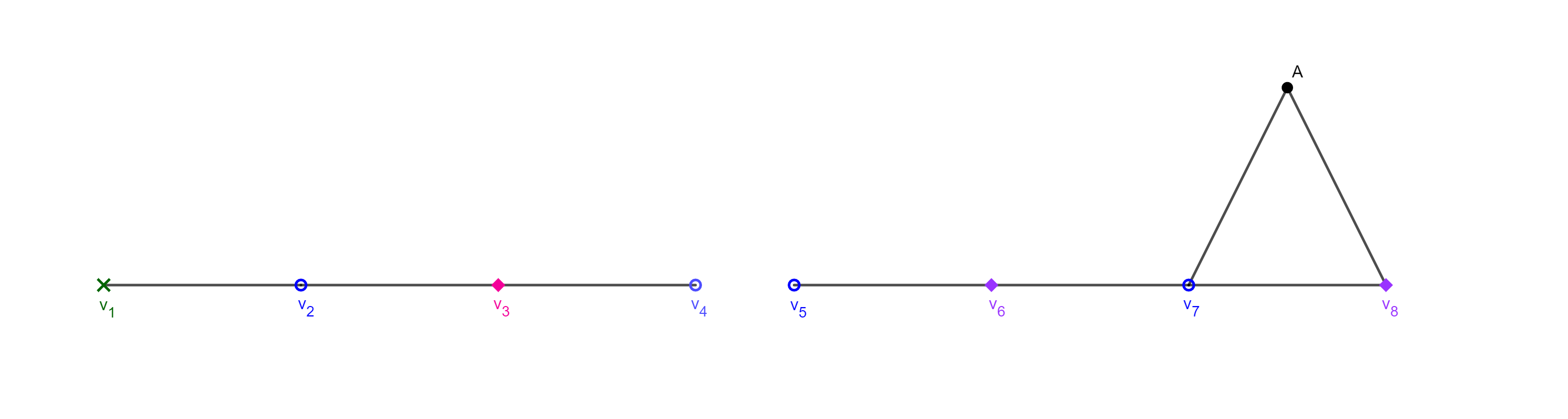
(d)

Suppose you presented player 2 with a chaing of four vertices. Player 2 colored the intial chain with two colors. You responded by adding $v_a\text{,}$ forcing a third color. You then presented a new chain of 4 vertices. Player two repeats the previous coloring so you add vertex $v_b\text{,}$ forcing a fourth color. You present a new chain of eight vertices. Player 2 repeats their previous coloring choices. What is your next move?

Solution

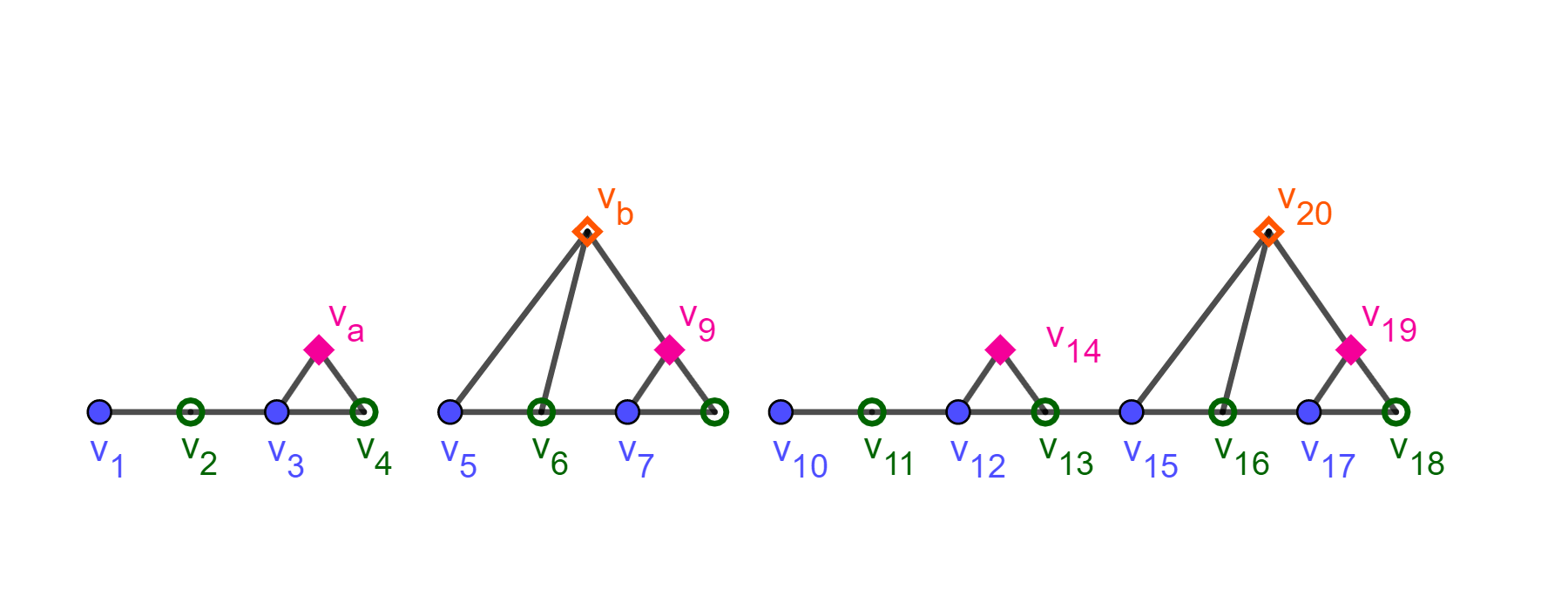
Add a vertex above and connected to the witnesses created this step.

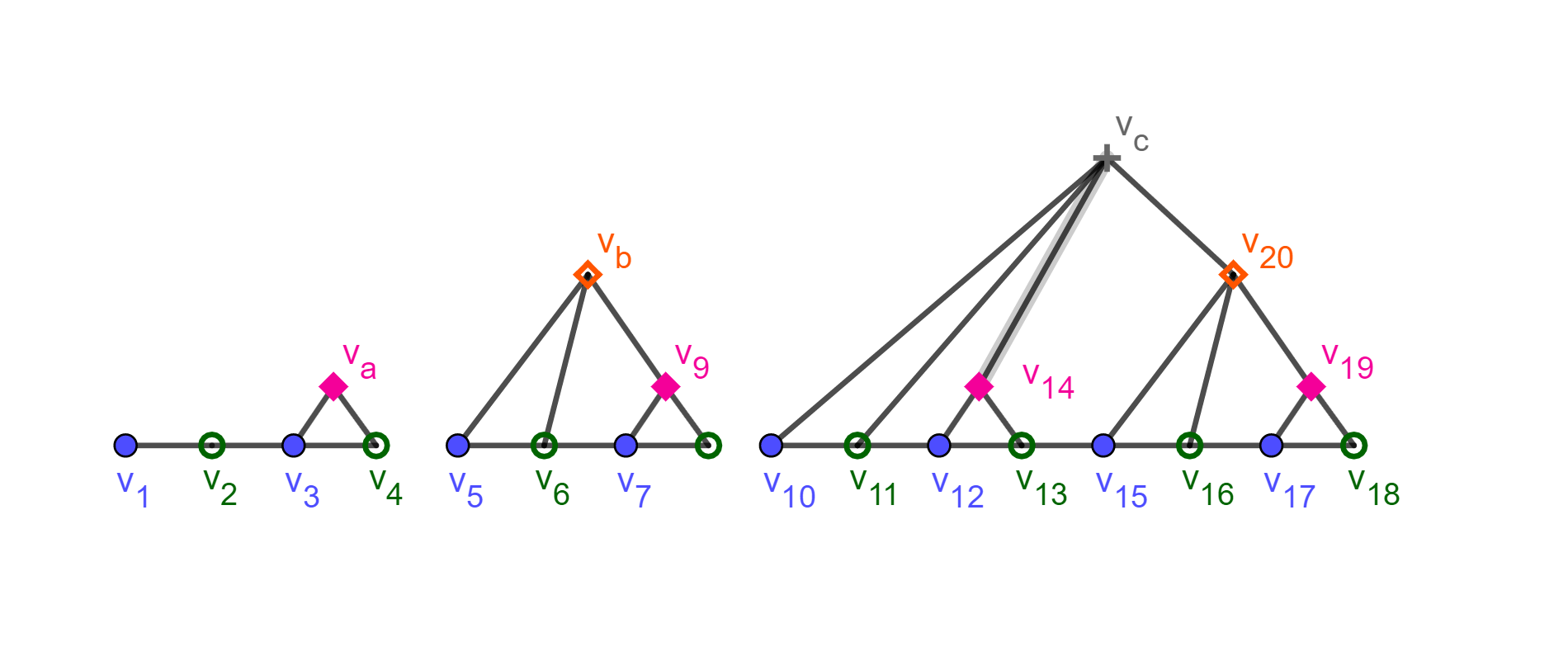
A key fact in our proof is relates the coloring graphs produced by the game above. In the following activity you will experiment with coloring such graphs.

Activity 22.

(a)

What is the chromatic number of this graph?

Solution

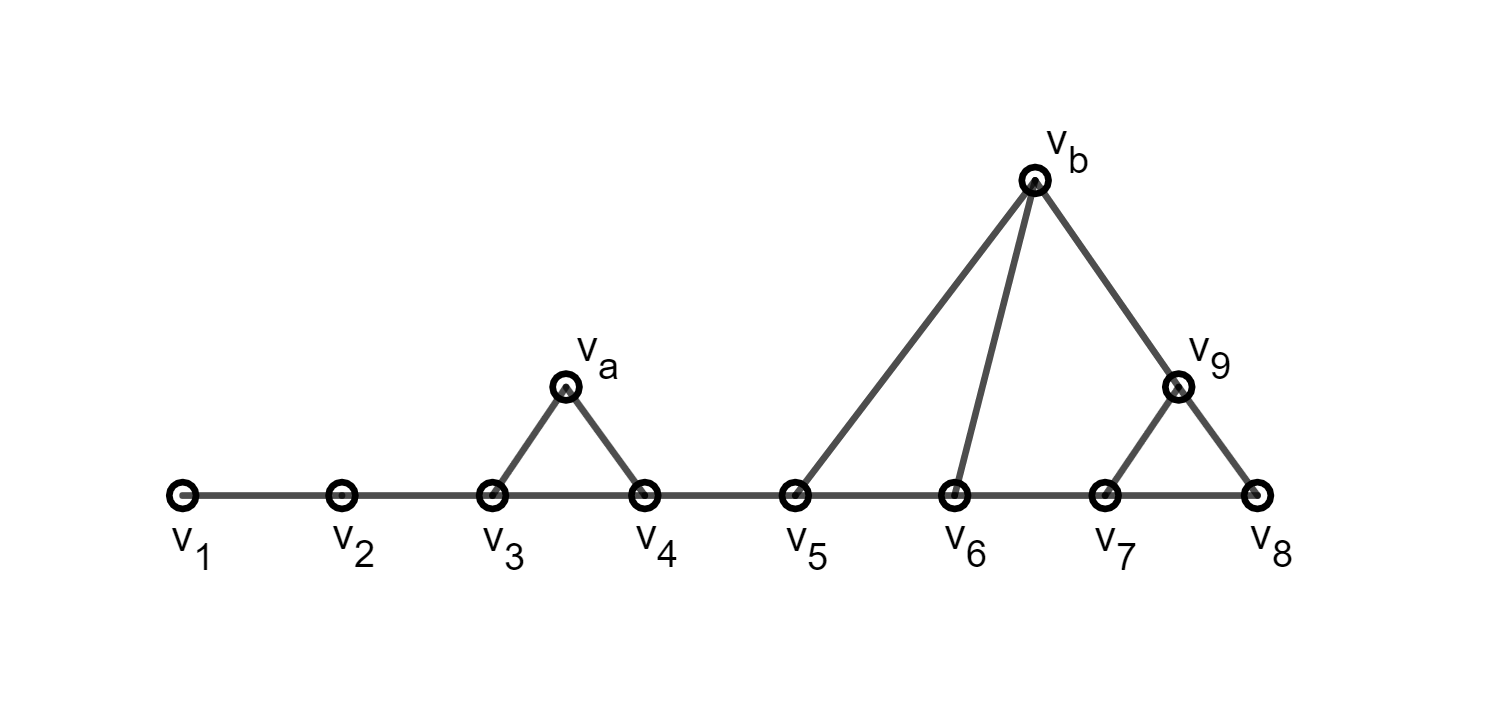
There are 3-cycles in the graph so it requires at least three colors. Here is one such three coloring:

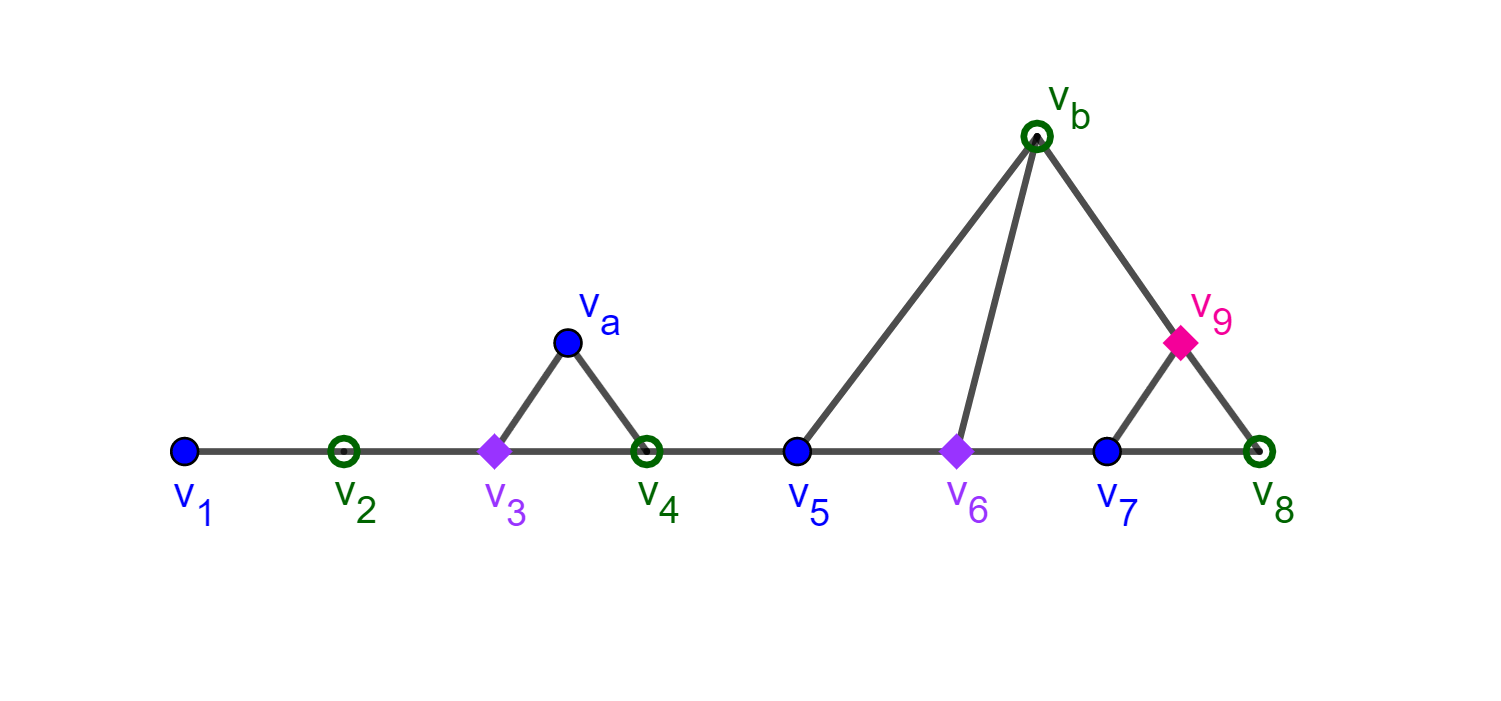
(b)

What is the chromatic number of this graph?

Solution

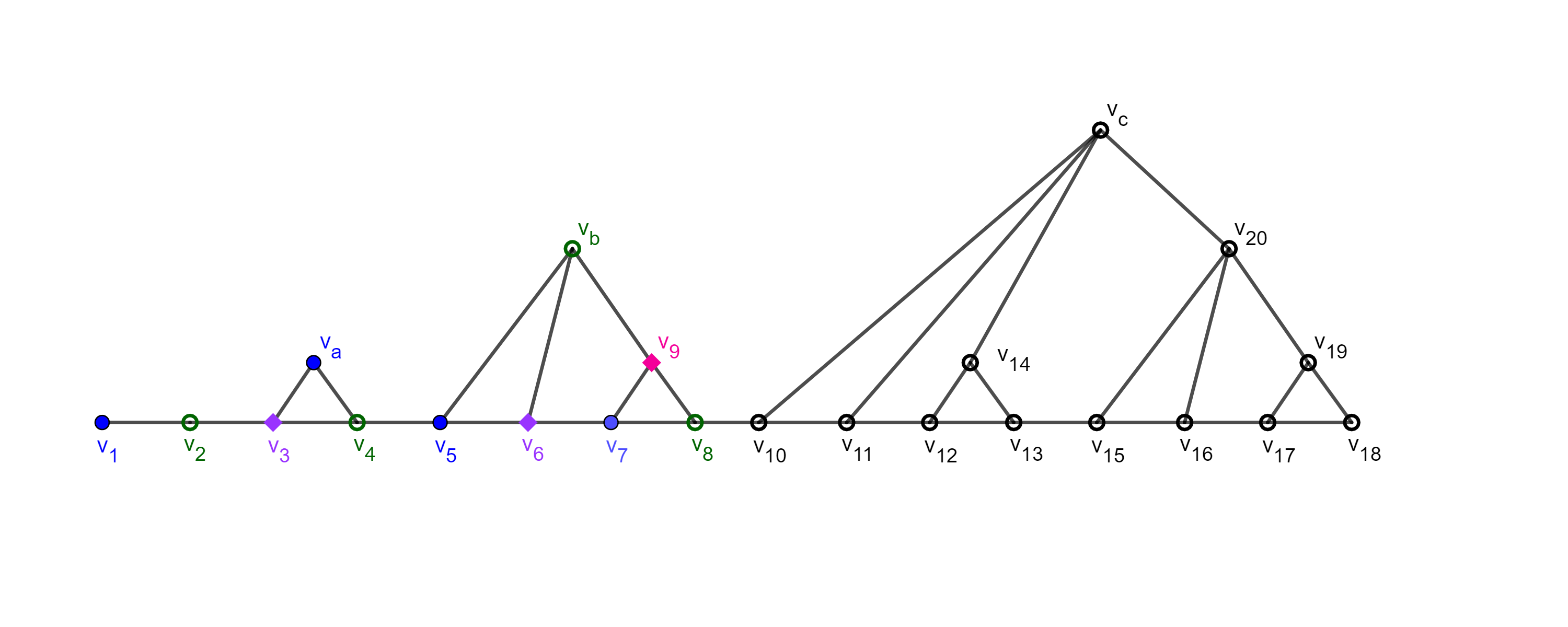
There are 3-cycles in the graph so it requires at least three colors. Here is one such three coloring:

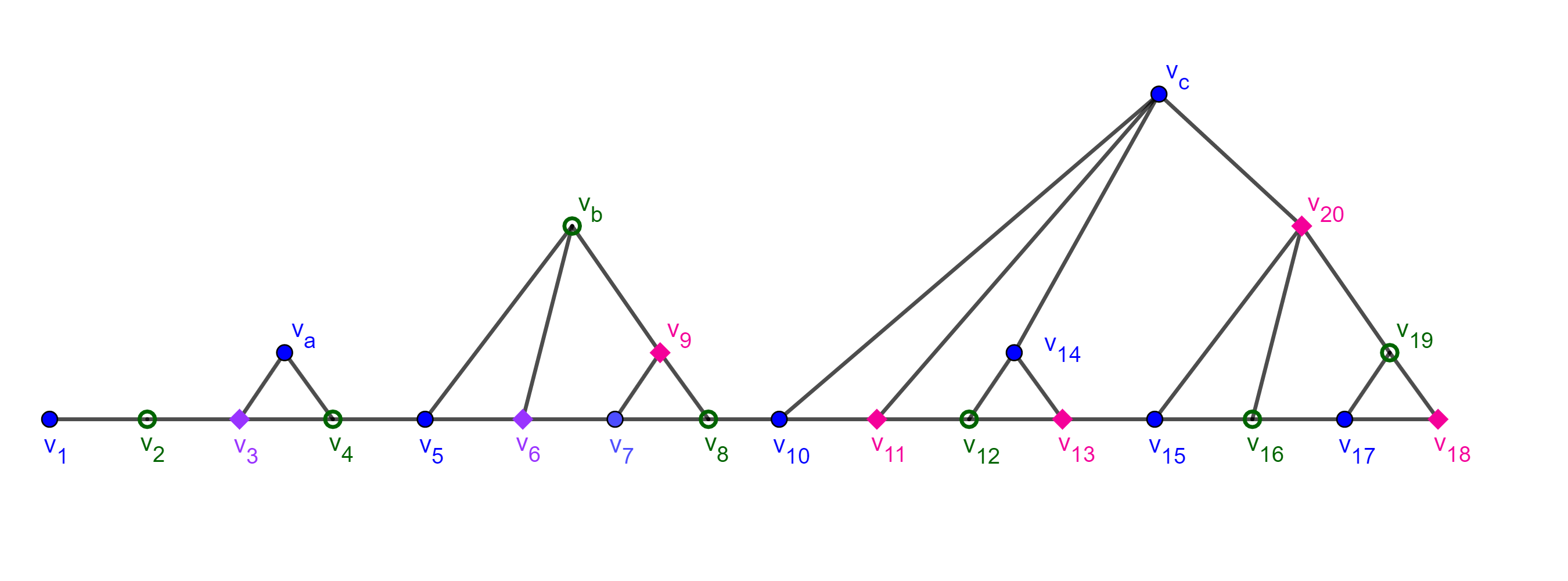
The previous activity suggests that any such graph can be 3-colored. This is true.

Lemma 7.2.3.

Any graph produced by the game above can be three colored.

Proof.

We will prove by induction. Note that in the base case the graph can be 3-colored with the witness vertices 2-colored.

Consider a graph $G_i$ that was produced using the game above. That graph will have one more witness vertex, $w$ than the previous graph, $G_{i-1}\text{.}$ By hypothesis $G_{i-1}$ can be three colored with all of it's witness vertices 2-colored, say colors 1 and 2. Color $w$ with color 1. Then rotate all the other colors, $1 \to 2\text{,}$ $2 \to 3\text{,}$ and $3 \to 1\text{.}$ $G_i$ is now 3 colored.

We are now ready to prove the main theorem.

Theorem 7.2.4.

There is a 3-colorable computable graph for which there is no computable $k$-coloring. The following proof is due to Bean.

Proof.

Now we will construct a computable graph $G$ that is not computably $k$ colorable but is 3-colorable. The construction is done in stages. At stage $n=s^e q$ where $q$ is odd a chain of $2^n$ vertices is appened to the corresponding chain added at the previous stage. Then consider the $2^e$ vertices $e_1, e_2, ..., e_{e^2}$ indroduced at stage $e$ and begin or contine the construction of the subgraph $G_e$ by formed by these vertices and any possible extensions above them.

Suppose the $\varphi_e$ is an algorithm for coloring of the graph. Then $\varphi_e^n$ will take the role of player II and we will take the role of player I.

$G$ is 3-colorable becuase it is composed of 3-colorable subgraphs, $G_e\text{.}$ $G$ is computable becuase vertices are never connect to each other after the stage at which they are introduced.

Suppose that $\varphi_e$ $k$-colors $G\text{.}$ Then at some stage in construction it will have used $k$ colors for $G_e\text{.}$ At the next stage a new color will be required so $\varphi_e$ cannot be a $k$-coloring of $G\text{.}$ Therefore $G$ is not $k$-colorable for any $k.$

Just as unfortunately, it ends up being the case that there exist bipartite graphs with $A$-perfect matchings where the matching is not computable. In fact, by focusing on a line graph (i.e., an infinite path; a bipartite graph which, for every vertex $v_{i}\text{,}$ $d(v_{i} )=2$), we will construct such a bipartite graph. Like the coloring game we played above, we may view the construction of this graph as a game as well, where again one player is constructing the graph and the other player is providing a matching of a vertex that must be part of the $A$-perfect matching of the graph. Here is how the game is played: The players will again turns. Player 2 is attempting to match a vertex in $A$ to a vertex in $B$ in such a way that the matching holds at every subsequent stage in the construction of the graph. Player 1 will construct the graph in such a way that Player 2 is forced to determine a different matching for that vertex in the next stage.

Player 1 presents the line graph on the vertices $a\text{,}$$b\text{,}$ and $c$ with $b\in A\text{.}$ Player 2 must determine a matching of $b$ to a vertex in $A$ that will persist as a matching for the duration of the construction of the infinite graph.
At this stage, Player 2 may choose to match $b$ to $a\text{,}$ match $b$ to $c\text{,}$ or claim that at this stage $b$ is unmatched. We will explore each of these options below.
During each subsequent stage, Player 2 may choose to match $b$ to $a\text{,}$ match $b$ to $c\text{,}$ match $b$ to another vertex, or claim that at this stage $b$ is unmatched.
Following any move by Player 2, Player 1 may add a vertex to either side of the current line graph to construct the next stage, or they may choose to add a vertex to both sides of the line graph.

In the following activity you will familiarize yourself with the game by playing a few rounds. You will again take the role of Player 1. You will be presented with a line graph represented the current stage of construction of our bipartite graph and a matching of the vertex $b$ given by Player 2. Your task is to construct the next stage of the graph, keeping in mind the rules described above.

Activity 23.

(a)

Suppose that you have presented the line graph below and Player 2 has decided $b$ is unmatched. What do you do?

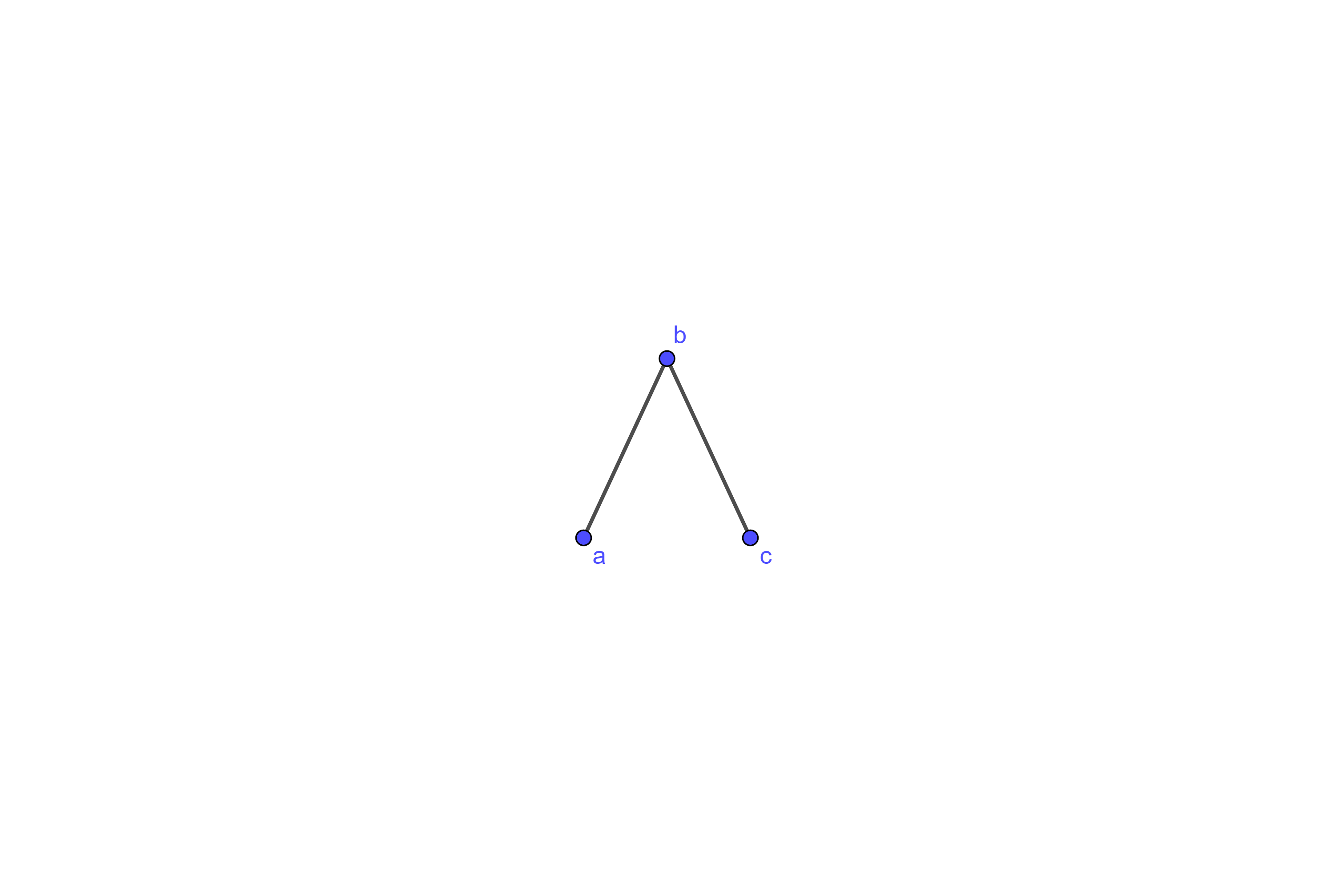
$Line graph with vertices $a\text{,}$ $b\text{,}$ and $c$ with $b\in A$$

Solution

If $b$ is unmatched at this stage, then at a vertex to either side of the line graph and $b$ will remain unmatched.

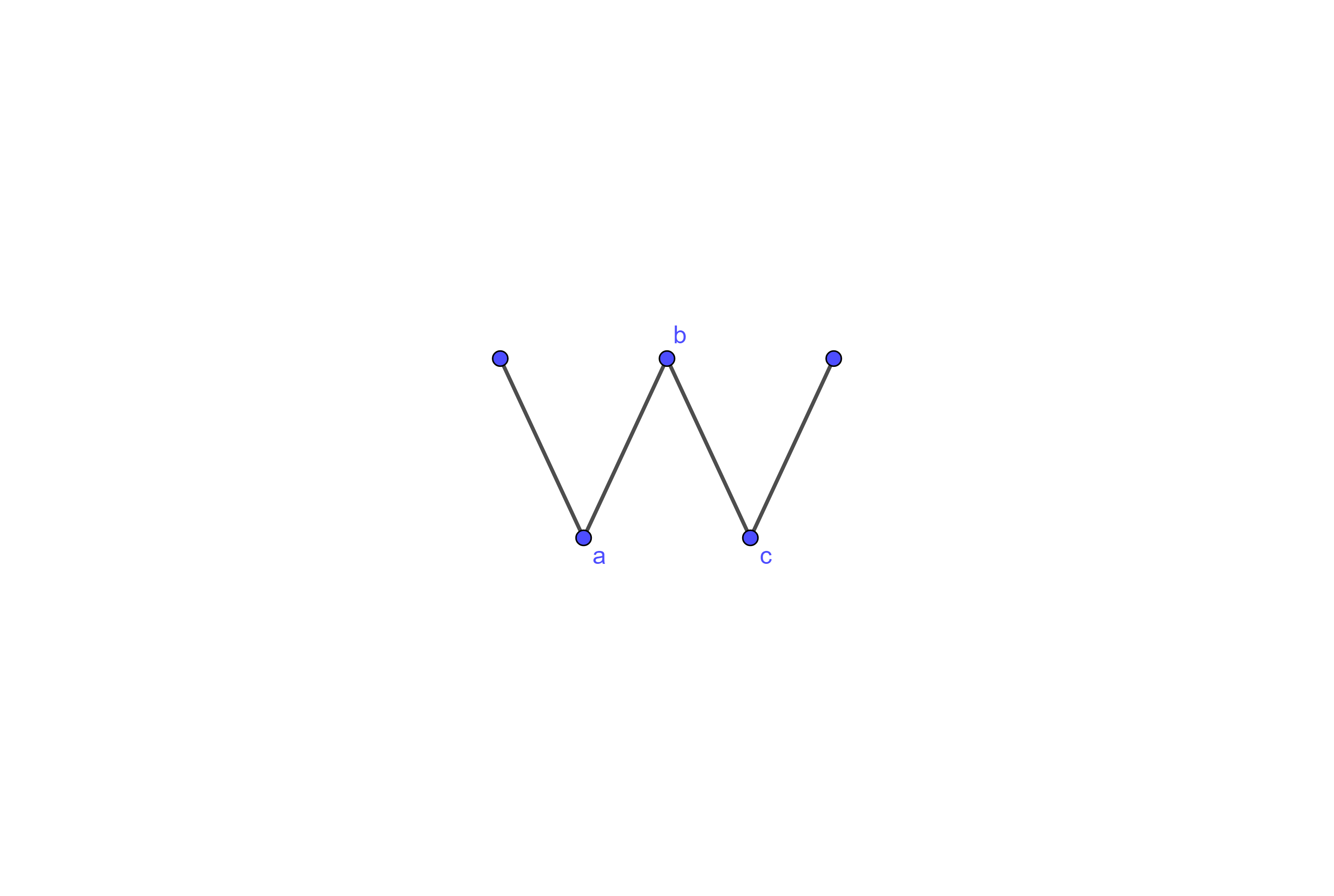
(b)

Suppose that you have presented the line graph below and Player 2 has decided $b$ is matched to $a\text{.}$ What do you do?

$Line graph with vertices $a\text{,}$ $b\text{,}$ and $c$ with $b\in A$$

Solution

If $b$ is matched to $a$ at this stage, then adding a vertex to the left prevents this matching from being part of an $A$-perfect matching at the next stage.

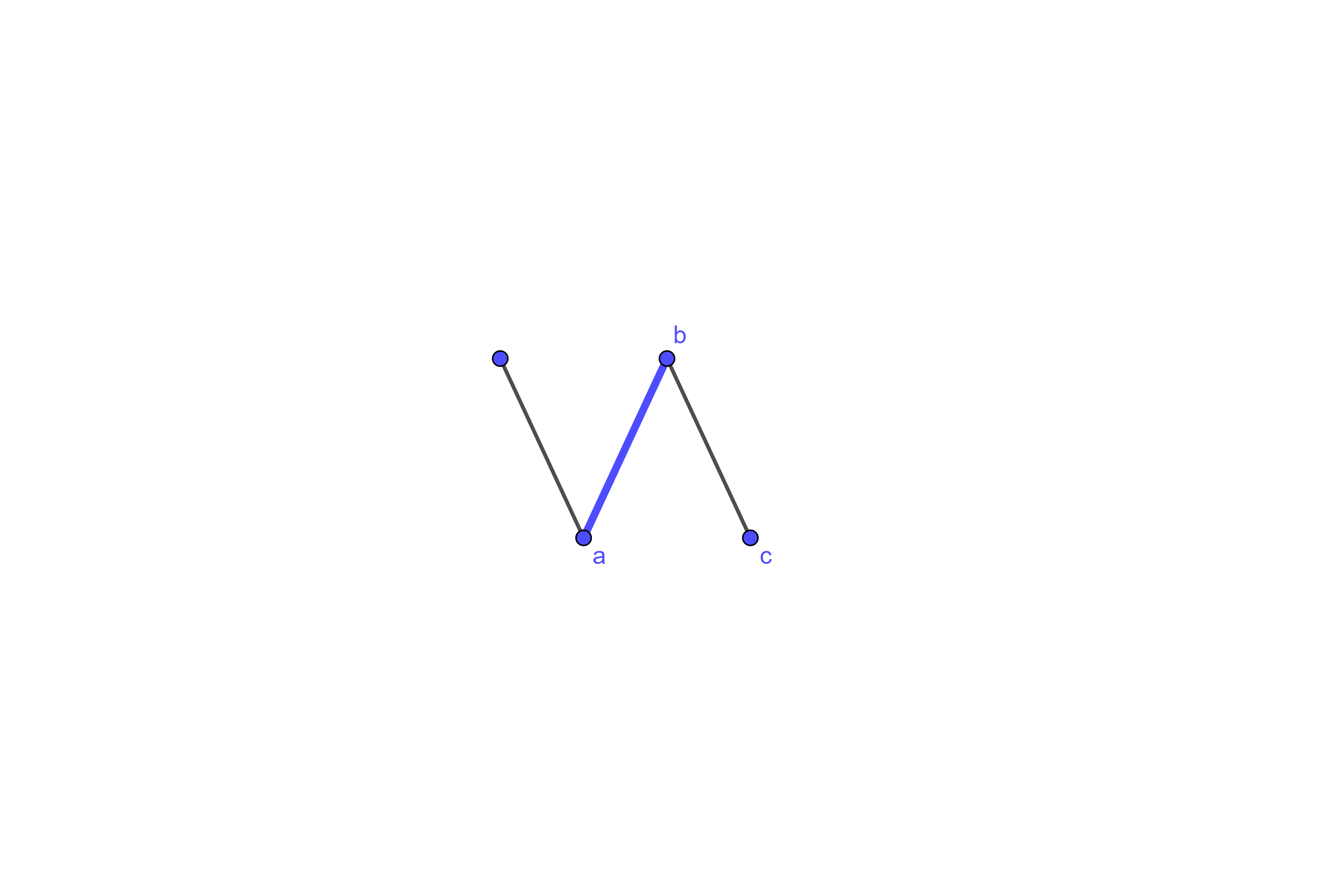
Note that in the above activity, if $b$ were matched to $c$ that you could proceed in similar fashion by adding a vertex to the right of the current line graph.

Now we'd like to look at arbitrary stages in our construction and determine what our next move would be.

Activity 24.

(a)

Suppose that you have presented the line graph below and Player 2 has decided $b$ is unmatched, or that $b$ is matched to a vertex that isn't $a$ or $c\text{.}$ What do you do?

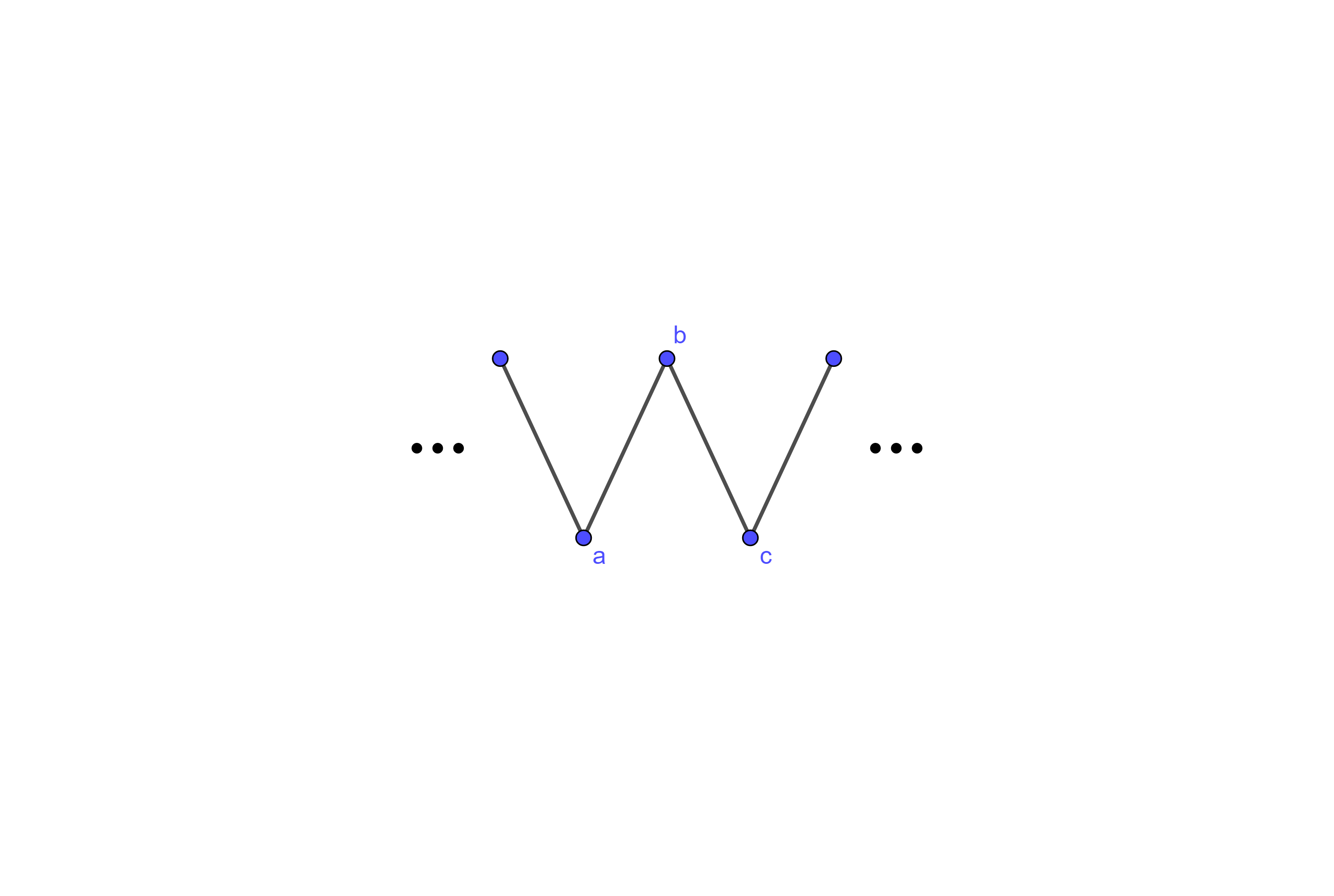
$Line graph at stage $s$ in construction with $b\in A$ unmatched$

Solution

If $b$ is unmatched at this stage, then add a vertex to either side of the line graph and $b$ will remain unmatched. If it is matched to a vertex not $a$ or $c\text{,}$ then add a vertex to both sides as this cannot be part of an $A$-perfect matching of the graph.

(b)

Suppose that you have presented the line graph below and Player 2 has decided $b$ is matched to $a\text{.}$ What do you do?

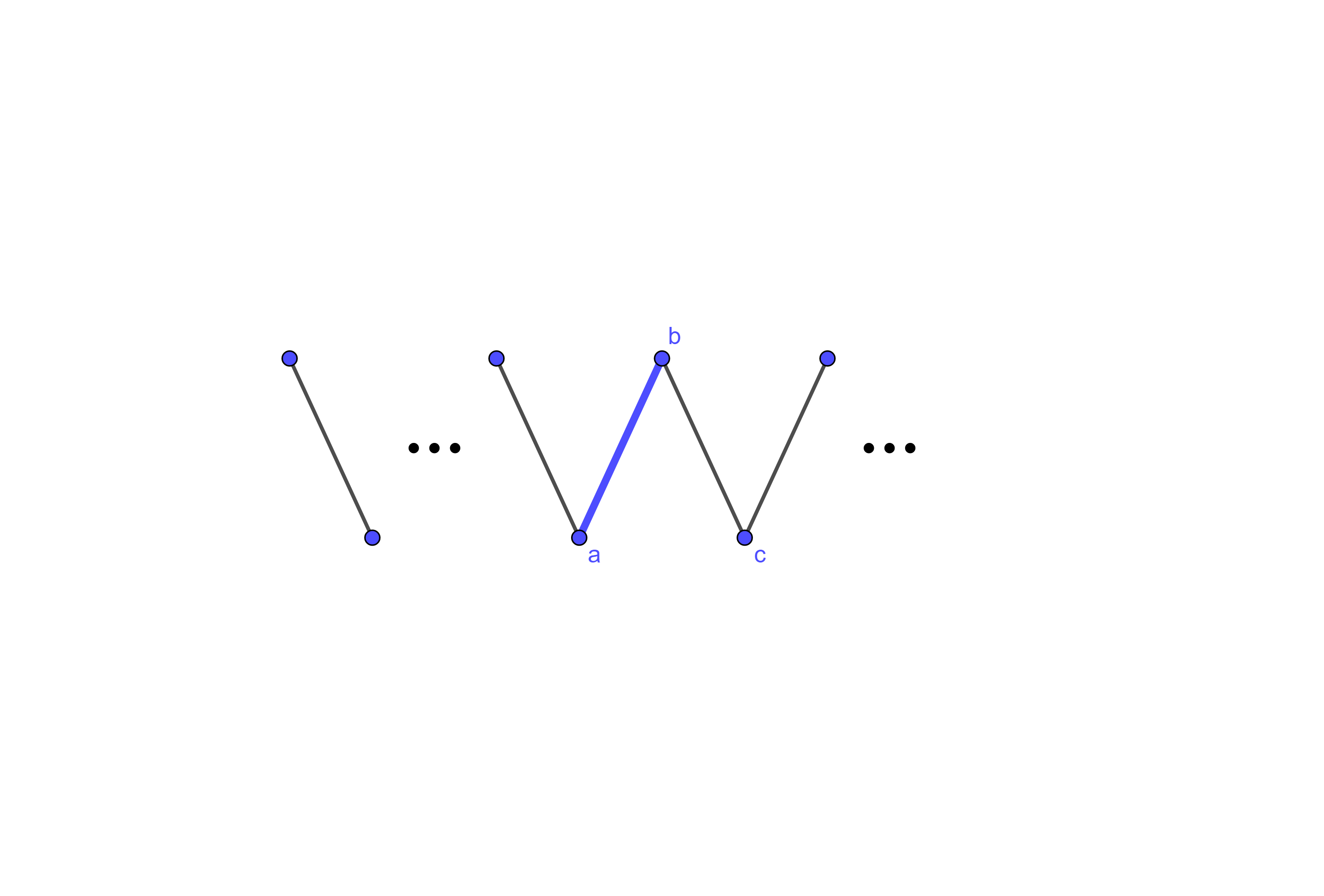
$Line graph at stage $s$ in its construction with $b\in A$ and $b$ matched to $a$$

Solution

Note that there must be an odd number of vertices to the left of $a\text{.}$ Then if $b$ is matched to $a$ at this stage, then the matching is already not part of an $A$-perfect matching at this stage. Then adding a vertex to the right prevents this matching from being part of an $A$-perfect matching at the next stage as well.

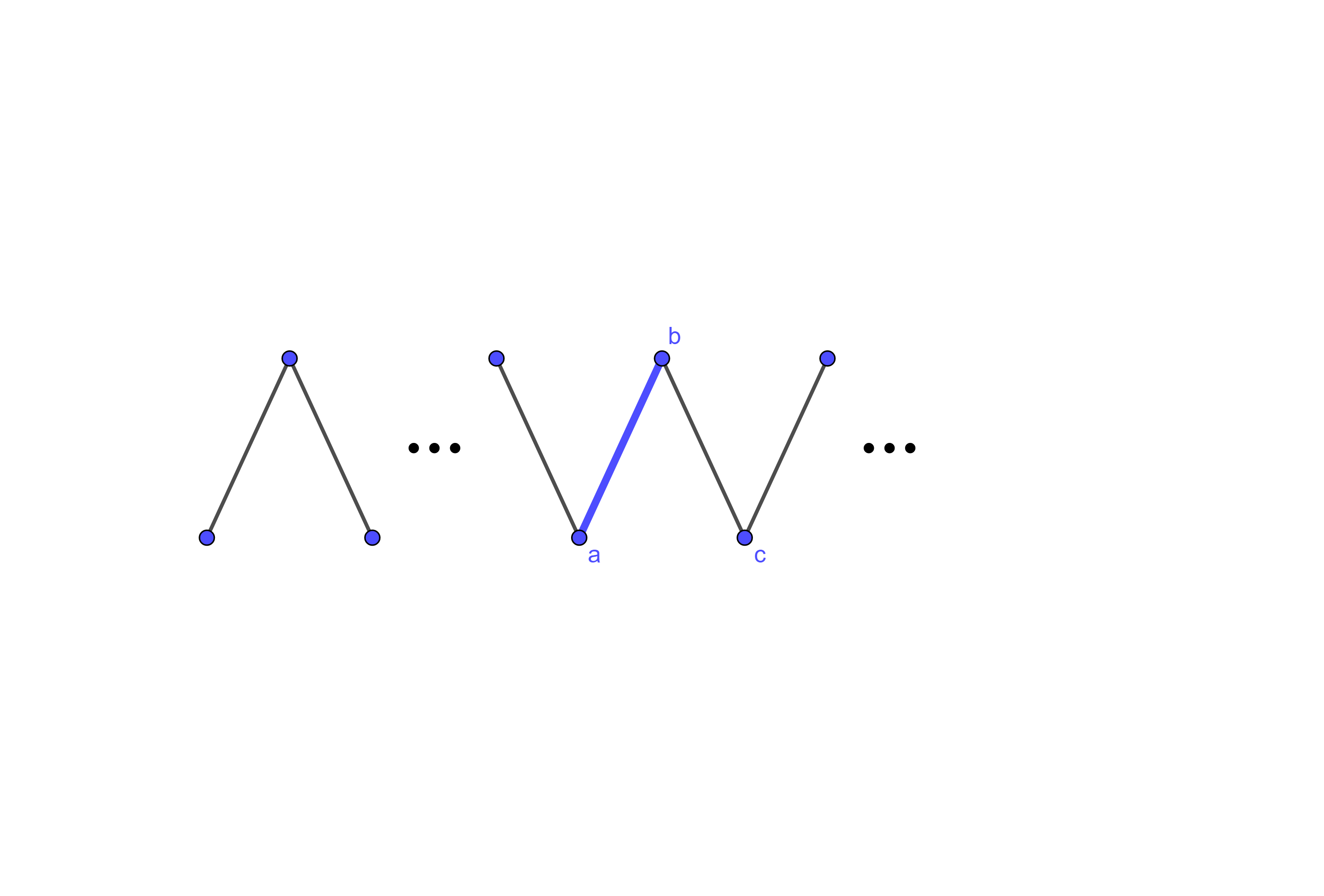
(c)

Suppose that you have presented the line graph below and Player 2 has decided $b$ is matched to $a\text{.}$ What do you do?

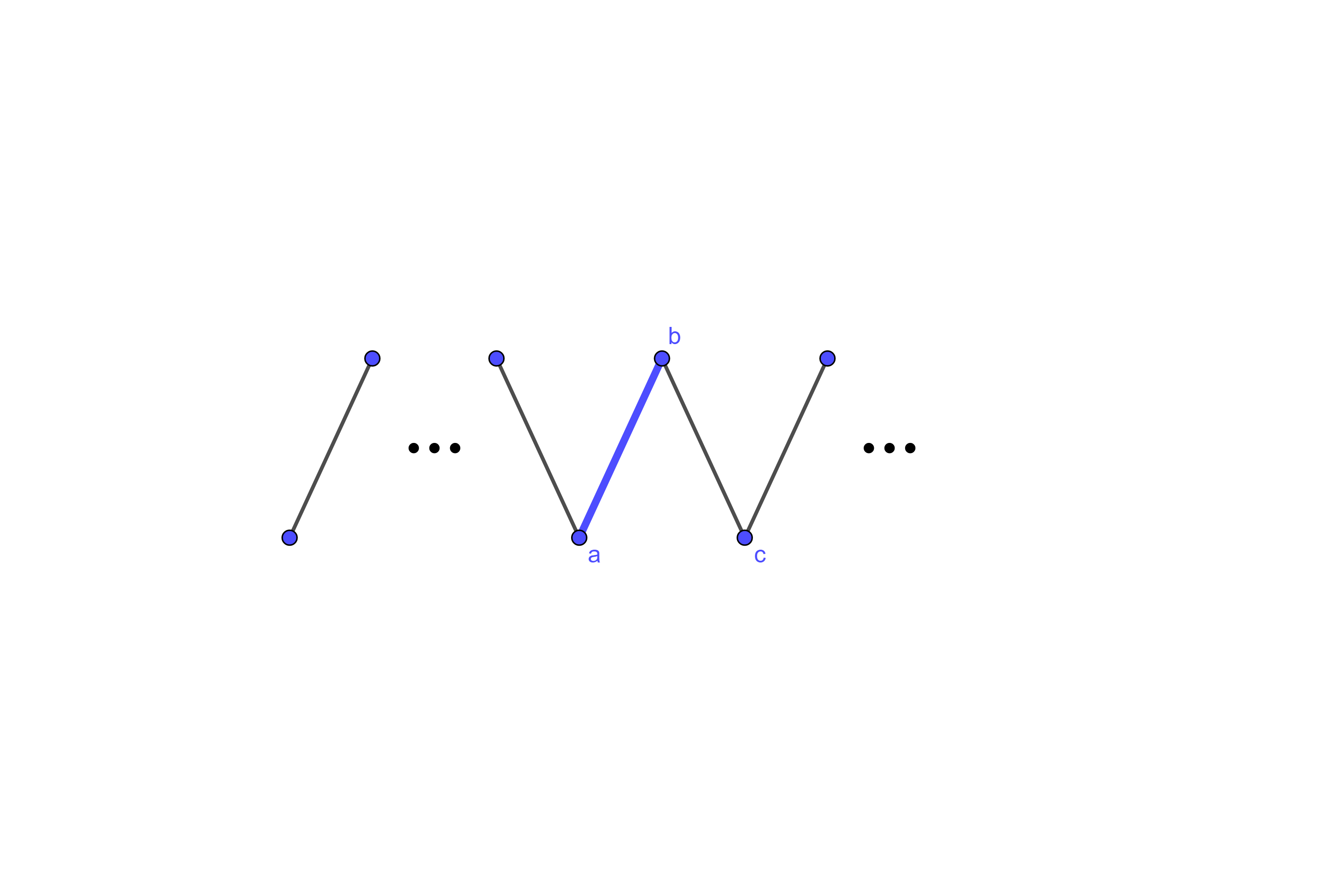
$Line graph at stage $s$ in its construction with $b\in A$ and $b$ matched to $a$$

Solution

Note that there must be an even number of vertices to the left of $a\text{.}$ Then if $b$ is matched to $a$ at this stage, then adding a vertex to each end of the line graph prevents this from being an $A$-perfect matching at the next stage of construction.

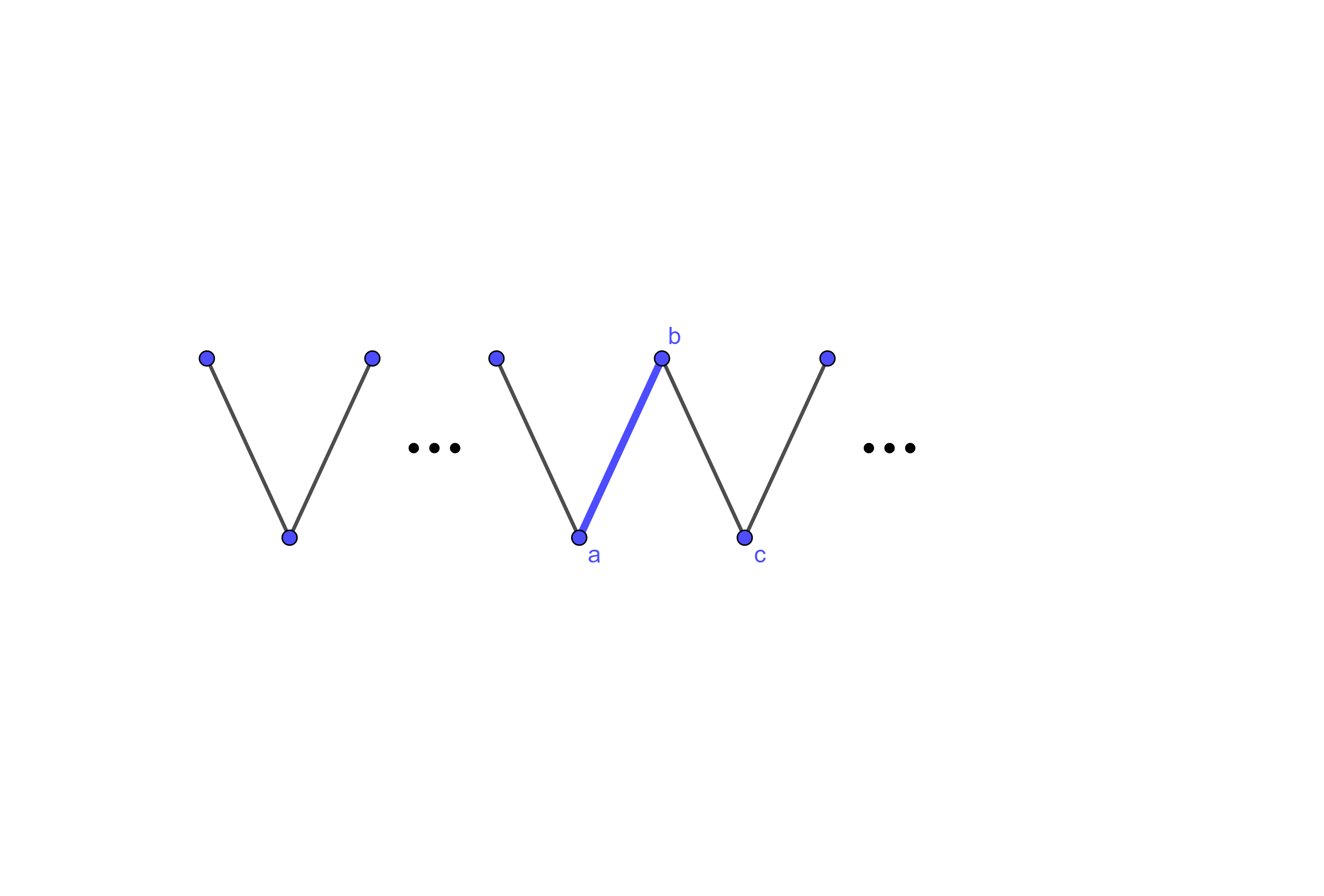
Note that we could similarly have had $b$ matched to $c$ in the two latter cases above, in which case we would attend to the graph to the right of $c$ to guide our construction.

You should verify that in each of your constructions above, that your graph is highly-computable at each stage, that the graph has a solution at each stage, and that the matching chosen by Player 2 is not an $A$-perfect matching of the graph.

Before giving a formal proof of the theorem you explored in these activities, we should define some terms.

Definition 7.2.5.

Let $G=(A,B,E)$ be a bipartite graph. $G$ is a computable bipartite graph if $A\text{,}$ $B\text{,}$ and $E$ are computable (that is, there exists an algorithm which can be used to determine whether a vertex $v_{i}$ belongs to $A$ or $B\text{,}$ and whether two given vertices $v_{i}$ and $v_{j}$ share an edge in $E\text{.}$)

Definition 7.2.6.

A number $e=\langle e_{1} ,e_{2} ,e_{3} \rangle$ determines a computable bipartite graph if $A=\{a|\{e_{1} \} (a)=1 \}$ and $B=\{b|\{e_{2} \} (b)=1 \}$ are disjoint. The computable bipartite graph determined by $e$ is $(A,B,E)\text{,}$ where $E=\{\{a,b \} |a\in A,b\in B,\{ e_{3} \}(a,b)=\{ e_{3} \} (b,a)=1 \}\text{.}$ (Here a notation $V=\{ v| \{e_{i} \}(v)=1 \}$ means that $V$ is the set of all vertices (or edges) which the algorithm $\{ e_{i} \}$ determines to consist of).

Definition 7.2.7.

Let $G=(A,B,E)$ be a bipartite graph. $G$ is a highly computable bipartite graph if $G$ is computable and the function $N_{G}$ is computable (that is, there exists an algorithm which can be used to determine all vertices adjacent to a given vertex $v_{i}$).

Definition 7.2.8.

A number $e=\langle e_{1} ,e_{2} ,e_{3} \rangle$ determines a highly computable bipartite graph if $A=\{a|\{e_{1} \} (a)=1 \}$ and $B=\{b|\{e_{2} \} (b)=1 \}$ are disjoint. The computable bipartite graph determined by $e$ is $G=(A,B,E)\text{,}$ where $E$ is determined by the fact that $\{ e_{3} \}$ computes $N_{G}\text{.}$

Lemma 7.2.9.

Let $G$ be the line graph on $(v_{i} ,v_{i-1} ,...,v_{1} ,x,y,z,w_{1} ,w_{2} ,...,w_{j} )\text{.}$ Interpret $G$ as being bipartite by assuming $y\in A\text{.}$ then we have:

If $i$ is odd then $(y,x)$ cannot be in any solution (matching) of $A$ to $B$ in $G\text{.}$
If $j$ is odd then $(y,z)$ cannot be in any solution of $A$ to $B$ in $G$

The proof is left to the reader. You should refer to the previous activity to aid in constructing this proof by induction.

Finally, we may construct a formal proof of the theorem from the preceeding activities.

Theorem 7.2.10.

There exists a highly computable bipartite graph $G=(A,B,E)$ such that for all finite $X\subseteq A\text{,}$ $|X|\leq |N_{G} (X)|\text{,}$ but $G$ has no computable solution (i.e., $G$ satisfies Hall's condition, but there exists no algorithm that allows us to find the $A$-perfect matching from $A$ to $B$).

Proof.

We construct a highly recursive bipartite graph $G$ determined by the number $e\text{,}$ where $G$ is given by $G(e)=(A(e),B(e),E(e))\text{.}$

At any stage $s$ in our construction of $G$ determined by $e\text{,}$ and given the partial function $\varphi_{e}^{s}$ that determines the solution to $G(e)$ at stage $s$ in its construction (which we shall write as $G(e,s)$), the following hold:

$G(e)$ is highly computable.
$G(e)$ has a solution (i.e., a matching from $A(e)$ to $B(e)$).
The algorithm $\varphi_{e}$ is not a solution of $G(e)\text{.}$

Stage 0: Let $G(e,0)$ be the line graph on $(a,b,c)\text{,}$ interpreted as a bipartite graph by specifying $b\in A(e,0)\text{.}$

Stage $s+1\text{:}$ Assume inductively that $G(e,s)$ is a line graph. Run $\varphi_{e}^{s}$ to determine the solution to $G(e,s)\text{.}$ We have 4 cases.

$\varphi_{e}^{s} (b)$ has no solution or has a solution that isn't $a$ or $c\text{.}$ Then form $G(e,s+1)$ by adding one vertex to each end of $G(e,s)\text{.}$
$\varphi_{e}^{s-1} (b)$ had no solution and $\varphi_{e}^{s} (b)=a\text{.}$ Then if there is an even number of vertices strictly to the left of $a$ in $G(e,s)\text{,}$ construct $G(e,s+1)$ by placing one vertex on each end of $G(e,s)\text{,}$ and if there is an odd number of vertices strictly to the left of $a$ in $G(e,s)\text{,}$ then construct $G(e,s+1)$ by placing one vertex on the right end of $G(e,s)\text{.}$ Either way, in all future stages of construction never place a vertex on the left end of $G(e)$ again.
$\varphi_{e}^{s-1} (b)$ had no solution and $\varphi_{e}^{s} (b)=c\text{.}$ Then we construct $G(e,s+1)$ as in Case 2, but we attend to the number of vertices to the right of $c\text{.}$
$\varphi_{e}^{s-1} (b)=a$ or $\varphi_{e}^{s-1} (b)=c\text{,}$ then at a previous stage Case 2 or 3 must have occured so add a vertex to whichever side is permitted.

Note that for any vertex $p\text{,}$ since $A(e)$ and $B(e)$ are computable, if $p\in A(e)\cup B(e)\text{,}$ then we can construct the graph until $p$ appears in either $A(e)$ or $B(e)\text{.}$ Since all of the neighbors of $p$ will appear in the graph by the end of the next stage of construction, $G(e)$ is highly computable.

Since $G(e)$ is just a 1- or 2-way infinite line graph, it clearly has an $A$-perfect matching.

By construction, $\varphi_{e}$ is not a solution of $G\text{,}$ as if Case 1 occurs there is clearly not a solution and if Case 2 or Case 3 occurs, then $\varphi_{e}$ is forced not to be a solution by the preceeding Lemma.