Section 3.2 Hamilton Paths and Cycles
In the last section we discovered how to create paths and cycles that used every edge once. In this section we will explore paths and cycles where we want to visit each vertex once.
Definition 3.2.1.
A Hamilton path of a graph \(G \) is a path that includes every vertex of \(G \) exactly once. A Hamilton path that starts and ends at the same vertex is a Hamilton cycle.
Activity 13.
Which (if any) of the graphs below contain a Hamilton path? a Hamilton cycle?
The first graph has a Hamilton path, but no Hamilton cycle. The second graph has neither a Hamilton path or cycle. The third graph has a Hamilton path but not a cycle. The fourth graph has both a Hamilton path and cycle.
It turns out that finding Hamilton paths and cycles can be quite tricky in general, but we have discovered some conditions to tell when we have a Hamilton cycle. We will explore some of these condtions, and then discuss their limitations and usefulness later.
Theorem 3.2.2. The Path-Cycle Principle.
Let \(G\) be a graph with \(n \geq 3 \) and suppose that \(G \) contains a Hamilton path whose endpoints \(a \) and \(b \) satisfy \(d(a)+d(b) \geq n \text{.}\) Then \(G \) contains a Hamilton cycle.
Proof.
By assumption \(G \) has a Hamilton path. Label the vertices of the path by \(a, v_1, v_2, …, v_{n-3}, v_{n-2}, b \text{.}\) Since this is a Hamilton path we know that the path contains all the vertices of the graph \(G \text{.}\)
We want to show that there exists some \(i \) where \(1 \leq i \leq n-3 \) such that \(G \) contains the edges \(av_{i+1} \) and \(bv_i \text{.}\) If we could find such an \(i \text{,}\) then \(G \) would have the Hamilton cycle \(a, v_1, …, v_{i-1},v_i, b, v_{n-2}, v_{n-1},…v_{i+2}, v_{i+1} \text{.}\)
To show that this \(i \) exists, we will create two sets, \(A \) and \(B\) as follows. List all the vertices adjacent to \(a \) except the first (in the order of the Hamilton path). Subtract one from the index of each remaining vertex. Let \(A \) be the set of index numbers of these vertices. Next, list all the vertices adjacent to \(b \) except the last. Let \(B \) be the set of index numbers of the remaining vertices.
Notice that \(A\cap B \) is the set of \(i \) values that satisfy our condition. If we can show that \(A\cap B \neq \emptyset \text{,}\) then we are done. We will show this by counting vertices. From our construction, \(|A| = d(a)-1\) as it contains every vertex adjacent to \(a\) except the first. Similarly, \(|B| =d(b)-1 \text{.}\) This implies that each set must be nonempty because not including \(a\) and \(b \) there are \(n-2 \) vertices in \(G \) and we disregarded an additional vertex from each set in their construction so each set can have at most \(n-3 \) elements on its own. Recall that by assumption \(d(a)+d(b)\geq n \text{.}\) So, \(|A| + |B| \geq n-2 \text{.}\) This means that there must be at least one element in \(|A| \cap |B| \text{.}\) Therefore, there exists some \(i \) where \(1 \leq i \leq n-3 \) such that \(G \) contains the edges \(av_{i+1} \) and \(bv_i \text{,}\) and hence \(G \) contains a Hamilton cycle.
Theorem 3.2.3. Bondy-Chvatal Theorem.
Let \(G\) be a graph with \(n\) vertices, where \(n\geq 3\text{,}\) and suppose that \(G\) can be expanded to a larger graph \(G'\) that contains a Hamilton cycle, by adding edges one at a time in such a way that an edge can be added by joining vertices \(A\) and \(B\) if \(A\) and \(B\) are not already adjacent and if their degrees satisfy \(d(A) + d(B)\geq n\text{.}\) Then \(G\) contains a Hamilton cycle.
Proof.
Proceed by contradiction. Suppose that \(G\) does not contain a Hamilton cycle. By the process described above for adding edges to create \(G'\) (which contains a Hamilton cycle), at some step in the process \(G_k\) is the last graph extension step that still does not contain a Hamiltonian cycle. Let the edge \(AB\) be the edge that is added to go from \(G_k\) to \(G_{k+1}\text{.}\) If the edge \(AB\) were not in the Hamilton cycle, then the graph \(G_k\) would contain a Hamilton cycle. Thus \(AB\) is part of the Hamilton cycle.
Since the \(AB\) edge was added to create \(G_{k+1}\text{,}\) we know in \(G_k\text{,}\) \(d(A)+ d(B) \geq n\) since that condition is necessary for an edge to be added. Observe since \(G_{k+1}\) contains a Hamiltonian cycle containing \(AB\text{,}\) then there is a Hamilton path in \(G_k\) that starts with \(A\) and ends with \(B\text{.}\) Thus by the path cycle principle, \(G_k\) must contain a Hamilton cycle. A contradiction. Thus \(G\) must contain a Hamiltonian cycle.
Why is the Bondy-Chvatal theorem useful? What does it give us that the path-cycle principle did not?
Theorem 3.2.4. Dirac's Theorem.
Let \(G\) be a graph with \(n\) vertices, where \(n\geq 3\text{,}\) and suppose that each vertex has degree greater than or equal to \(n/2 \text{.}\) Then \(G\) contains a Hamilton cycle.
Proof.
Let \(G\) be a graph with \(n\) vertices, where \(n\geq 3\text{,}\) and suppose that each vertex has degree greater than or equal to \(n/2 \text{.}\) Add an edge between two non-adjacent vertices of \(G\) and continuing adding edges between non-adjacent vertices until it is no longer possible. The resulting graph have each pair of vertices \(d(A)+d(B)\geq n/2+n/2=n\text{.}\) Thus the Bondy-Chvatal theorem can be applied and so \(G\) contains a Hamilton cycle.
Why is Dirac's theorem useful? What does it give us that the Bondy-Chvatal theorem did not?
The limitations of Hamilton Cycles.
The above theorems give us some conditions that allow us to find Hamilton cycles, but none of them are very restricitive. Ideally, we would like a condition to use on a general graph that would tell us if we have a Hamilton cycle. Sadly, mathematicians have not found one yet. (This is what we call an open problem.) But why is that? What is it about Hamilton cycles that make it so difficult to find Hamilton cycles in general?Activity 14.
How many different Hamilton cycles can you find from a complete graph with 5 vertices? Solution 1There are 12 possible Hamilton cycles. To see why, label the vertices \(v_1\) through \(v_5 \text{.}\) You have 5 choices for the vertex you start at. Since all the vertices have edges between them, you then have 4 choices for the second vertex in the cycle, 3 choices for the third, 2 for the fourth, and one for the final. However, the cycle \(C = v_1 v_2 v_3 v_4 v_5 \) is the same as the cycle \(C_{shift} = v_2 v_3 v_4 v_5 v_1 \) and all other cycles with the vertices in the same order, but where the indices are shifted. It is also the same as the cycle \(C_{reverse} = v_5 v_4 v_3 v_2 v_1 \) where the order of the vertices are reversed and all the cycles with reversed order and shifted. So there are \(5!/5\cdot 2 =12\) Hamilton cycles.
Using the same reasoning we calculate that there are \(6!/6 \cdot 2 = 60 \) possible Hamilton cycles. So there are \(60-12 = 48 \) additional possible Hamilton graphs from adding one vertex.
This activity demonstrates the main problem: When we add vertices to a general graph, we gain an exponential number of potential Hamilton paths that we have to check. Since we do not have criteria to make it easier to narrow down potential paths, we have to check every path. That is a lot of paths! Even computers have trouble checking them all in a limited timeframe.
Applications.
Having a solution to when a graph has a Hamilton cycle would be groundbreaking. Companies and individuals could save resources if we could find Hamilton cycles.
Activity 15.
A national park has 11 sites that need to be visited every day by a staff member to ensure everything is functioning properly. Is there a route the staff member could take where they would only visit each site exactly once and end at where they started?
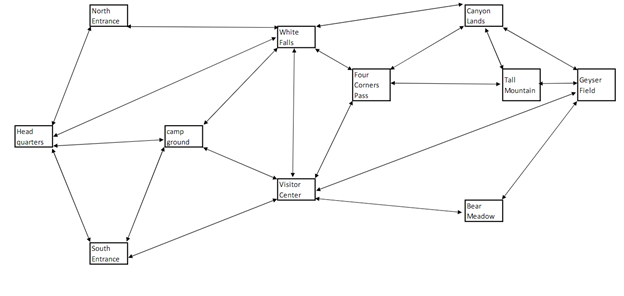
There are several solutions to this problem. Here are a couple: (1) North Entrance -> White Falls -> Four Corners Pass -> Canyon Lands -> Tall Mountain -> Geyser Field -> Bear Meadow -> Visitor Center -> Camp Ground -> South Entrance -> Head Quarters -> North Entrance (2) North Entrance -> White Falls -> Canyon Lands -> Four Corners Pass -> Tall Mountain -> Geyser Field -> Bear Meadow -> Visitor Center -> South Entrance -> Camp Ground -> Head Quarters -> North Entrance
These types of questions come up daily, and many times the graphs imposed on the situations do not meet the criteria we have for guarenteeing a Hamilton cycle. Further, if there are several possible Hamilton cycles, how would you go about picking which is the best to use? These are some of the complicated questions individuals and companies ask that could be answered if we knew more about Hamilton cycles.